Velocity Frequency Design

Introduction

After having a proper identification of the system plant, you can configure the control loop.

In this document you will see the most important parts of this wizard, and how to use it.

In order to perform the design the plant model must have been set in the previous step of the wizard, otherwise this page will be disabled.

Further technical information about how Velocity control loop works, click on here.

Overview of this page

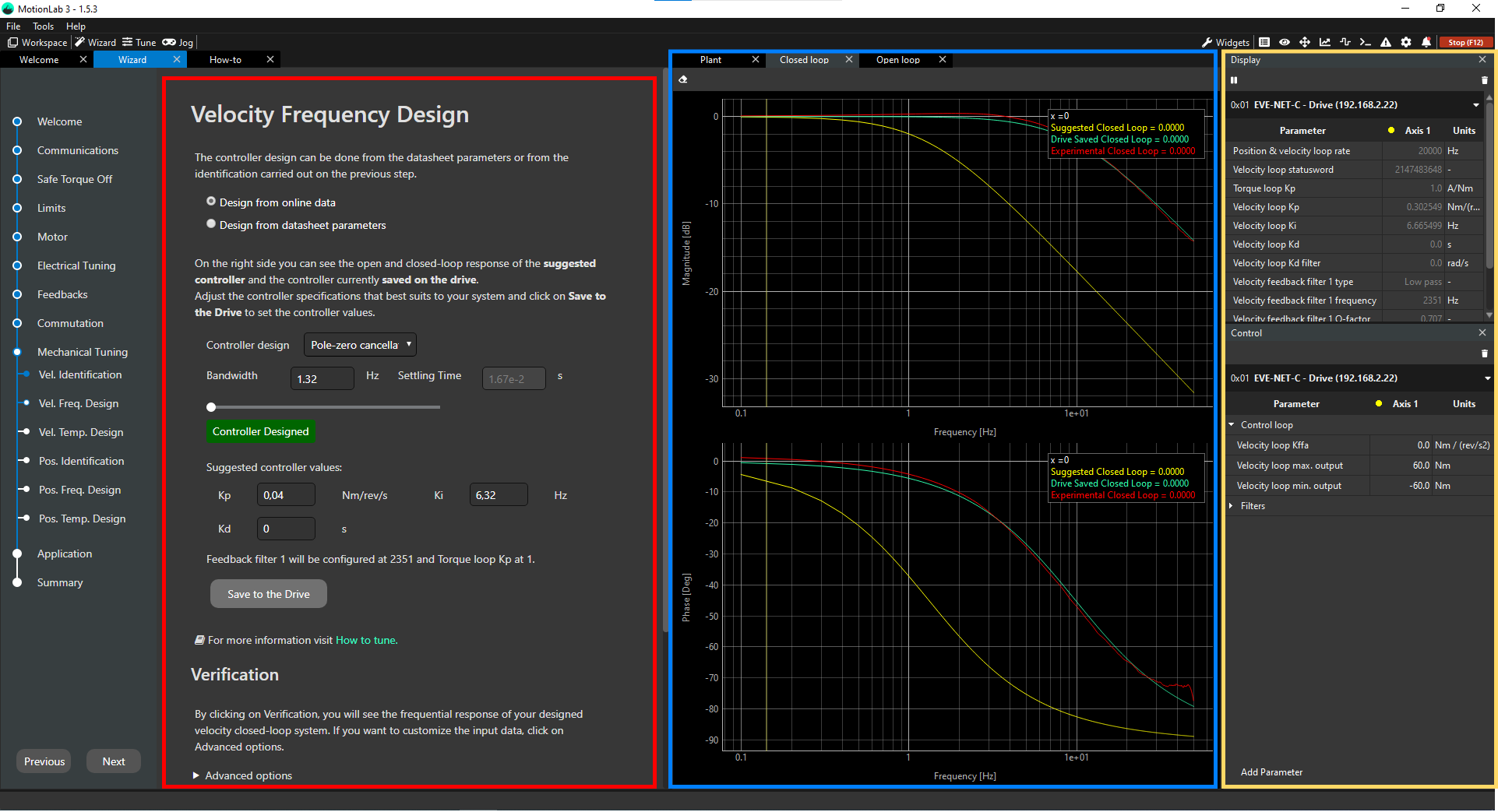
There are 3 parts on this wizard page:

• System configuration and verification (red).

• Bode diagrams of magnitude and phase (blue).

• Display and Control widgets (yellow).

System Configuration and Verification

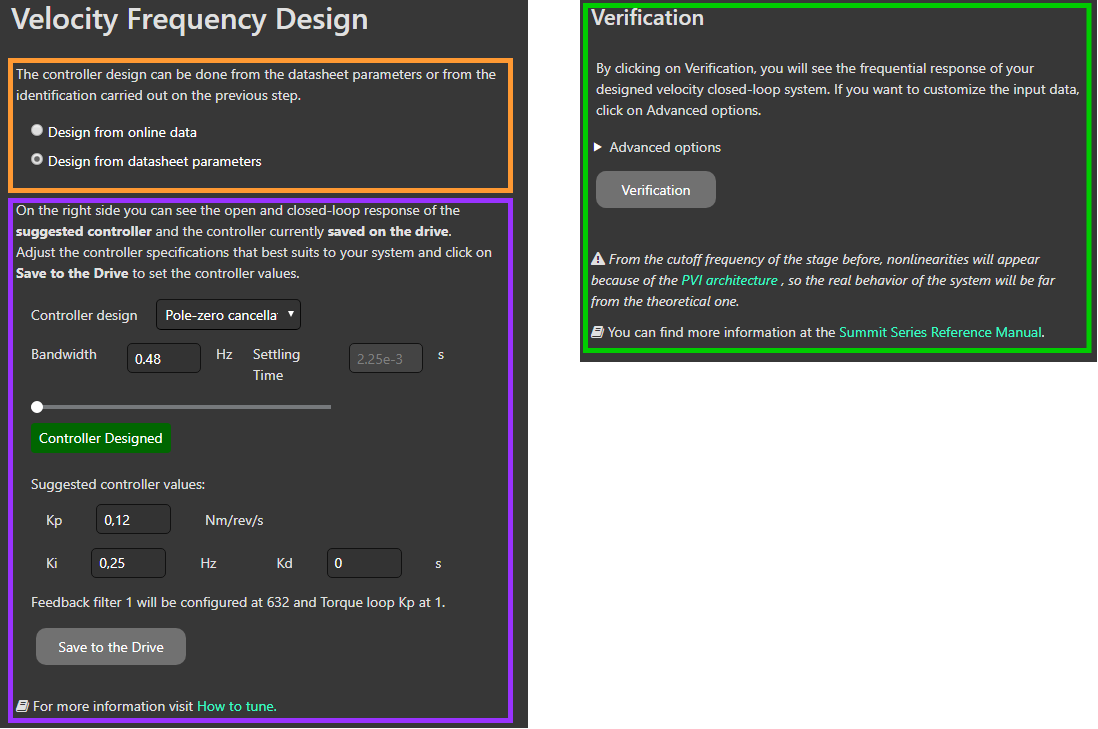
There are 3 main subparts:

• Plant model choice (orange).

• Bode diagrams of magnitude and phase (purple).

• System verification (green).

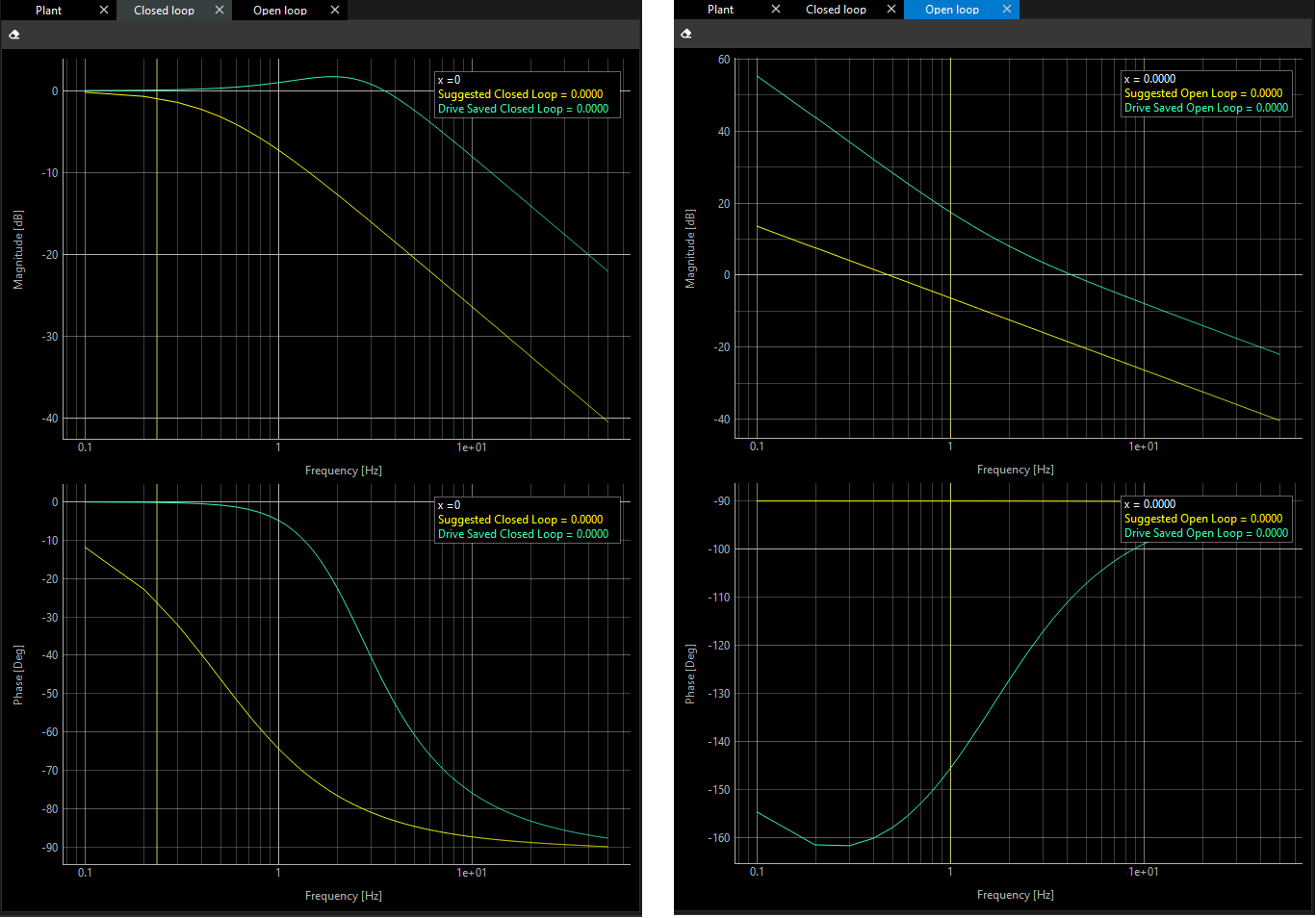
Bode diagrams of magnitude and phase

You have two tabs:

• Closed loop

• Open loop

Both tabs show the Gain and Phase in frequency domain.

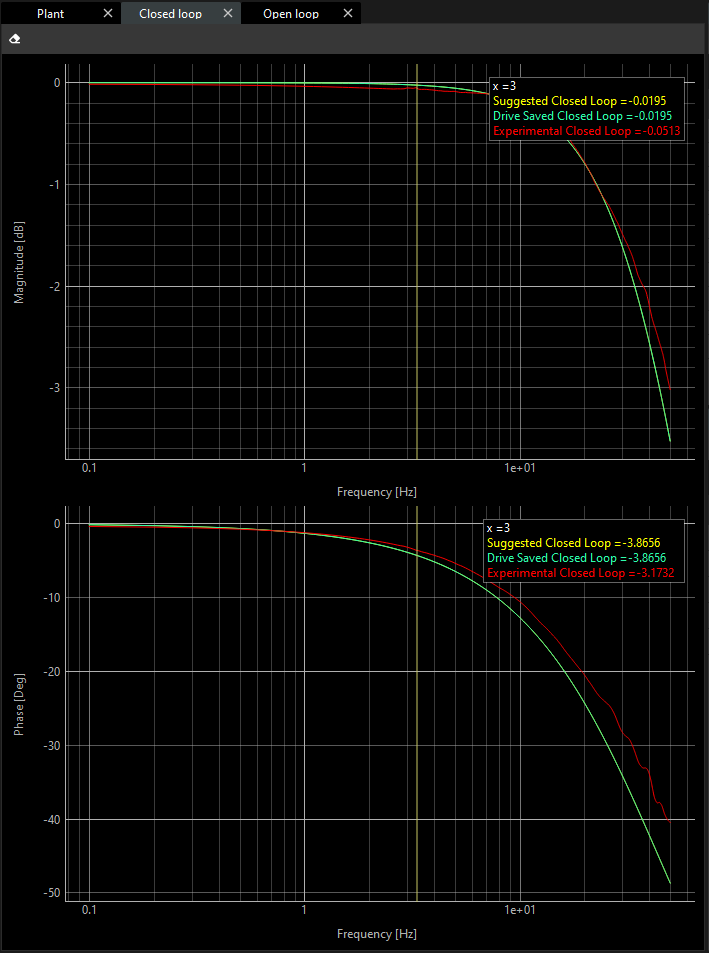
The Closed Loop Transfer Function (CLTF) is the most common way to describe the control system in the frequency domain. The data is taken while the loop is closed, so all of the closed loop dynamics are captured in this transfer function. The gain of the CLTF is very close to unity at low frequency and rolls off at high frequency, with some amplification in between. The phase of the CLTF is near 0 at low frequency and near -180 degrees at high frequency. This curve is typically used to state the system’s “Bandwidth”.

The Open Loop, or “Loop” transfer function (OLTF) is representative of all the frequency dependent blocks that make up of the servo loop, meaning the control, the drive, the plant, and the sensor. The OLTF for some systems can be taken with the servo loop open, but in many cases it must be either derived from the Closed Loop, or taken with the loop closed, and done so using the test point. The OLTF can be found from the Closed Loop using the formula CLTF/(1-CLTF), where CLTF is the complex representation of the closed loop transfer function. The CLTF can be measured by driving the system with random or swept sine at In2 and measuring Out2/In2. The OLTF can be found by driving with In2, but measuring Out2/Out3. The open Loop and closed loop transfer function are shown below.

Plant model choice

Depending on the identification method used on previous page, Velocity tuning: identification, you should select the model you want to use to design your controller.

1. If theoretical identification was used, the only option will be design from datasheet.

2. If experimental identification was used, the only option will be design from estimated model.

3. If both were used, both options will appear.

Loop adjustment

The main goal of this step is to adjust the loop parameters: K_p, K_i and K_d. You can get them and simulate their implications for the system without saving in the drive. You will be able to see these simulations in different plots.

Once you consider these parameters work properly, you can save them into the drive. You can see further below several examples about how the closed loop behaves with different K_p's , K_i's and K_d's.

You can see here an example how different the different parameters can affect your system.

Methods

In order to do that you have to choose which methodology you want to apply.

There are 3 methods:

• Pole placement

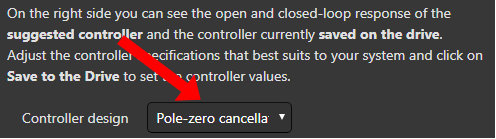
• Pole-zero cancelation

• Manual

Pole-zero cancellation and Pole-placement are automatic methods that calculate the K_p, K_i and K_d. Manual is to adjust the parameters manually and see the frequential response.

For more information about these parameters, go to the How to Tune page.

Pole placement

You will see the following in this part.

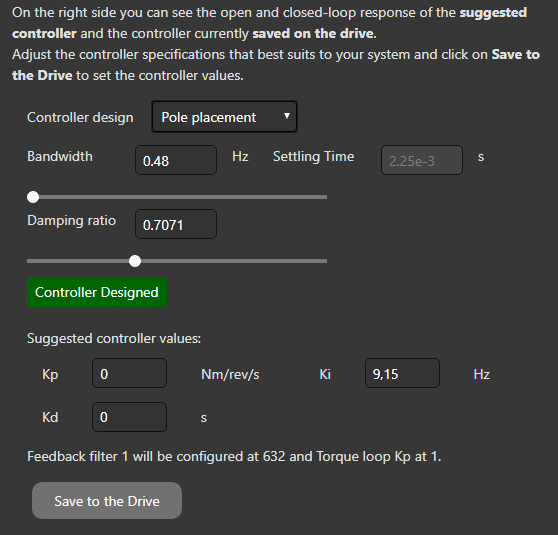
You can adjust K_p, K_i and K_d moving both sliders: Bandwidth and Damping ratio.

Go to How to tune - Bandwidth section and Damping section, for further information about these parameters.

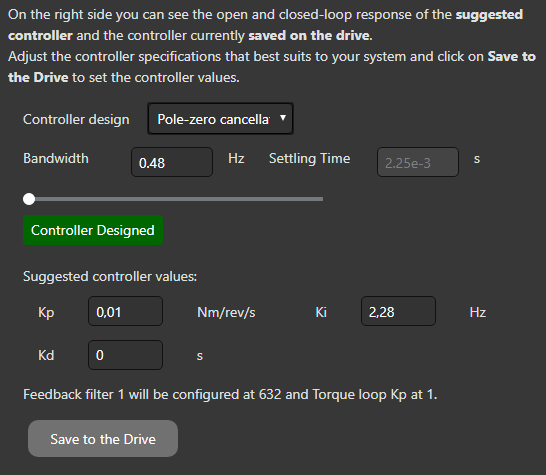
Pole-zero cancelation

If you think you don’t need the Damping parameter, you can use this method using only the Bandwidth parameter.

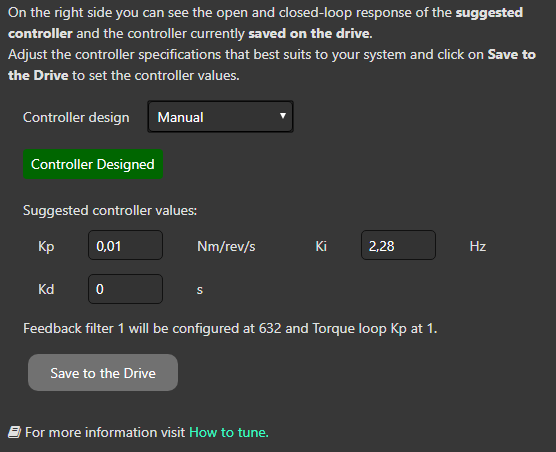
Manual

Here, you can modify K_p, K_i and K_d directly without any without adding a calculation based on the desired bandwidth and damping.

Example

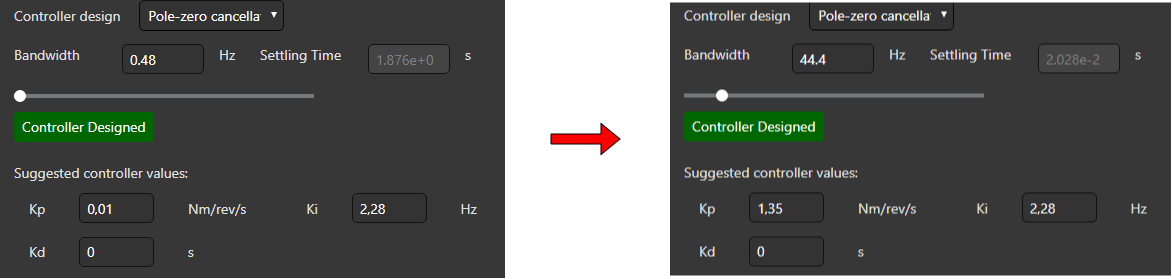
In the case of Pole-zero cancellation.

If you move the Bandwidth slider or directly you edit the its value directly, K_p, K_i and K_d parameters will be modified automatically.

The label under the slider indicates the stability of the system

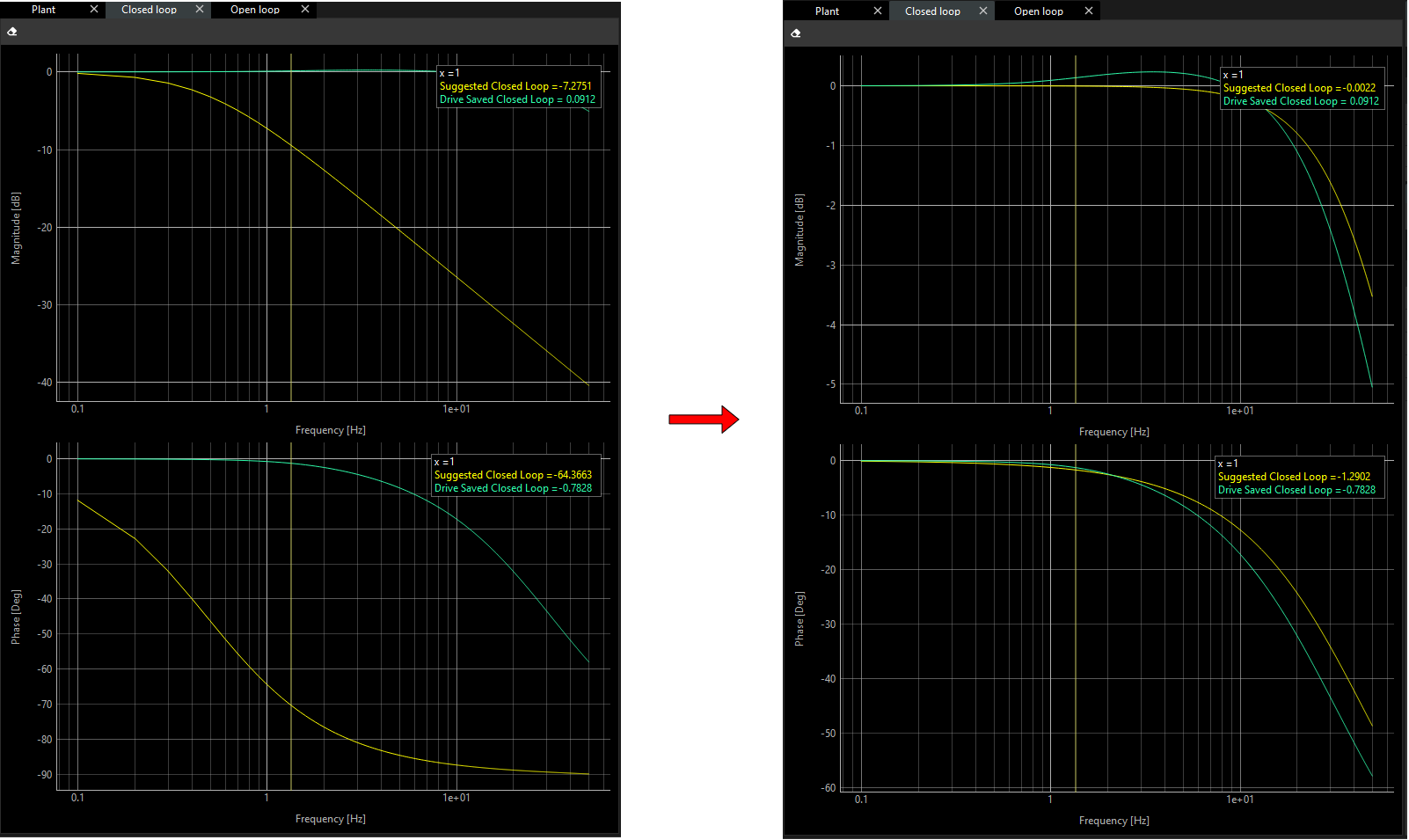
Check the frequential response of your system and adjust the slider until the expected result is obtained. Also, you can compare the response of the controller values saved on the drive against the suggested new ones.

For more information, go to the How to Tune page.

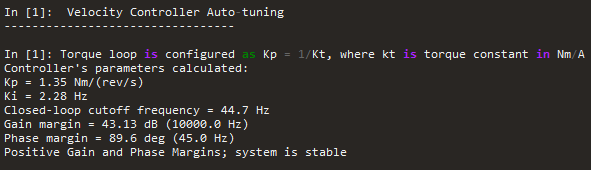
You have further information as well in the Terminal:

However, these loop parameters won’t be saved into your drive. You have to click on the button “Save to the Drive”.

In order to check if they are properly saved, you can see:

• Drive Saved Closed Loop plots change their shape like Suggested Closed Loop.

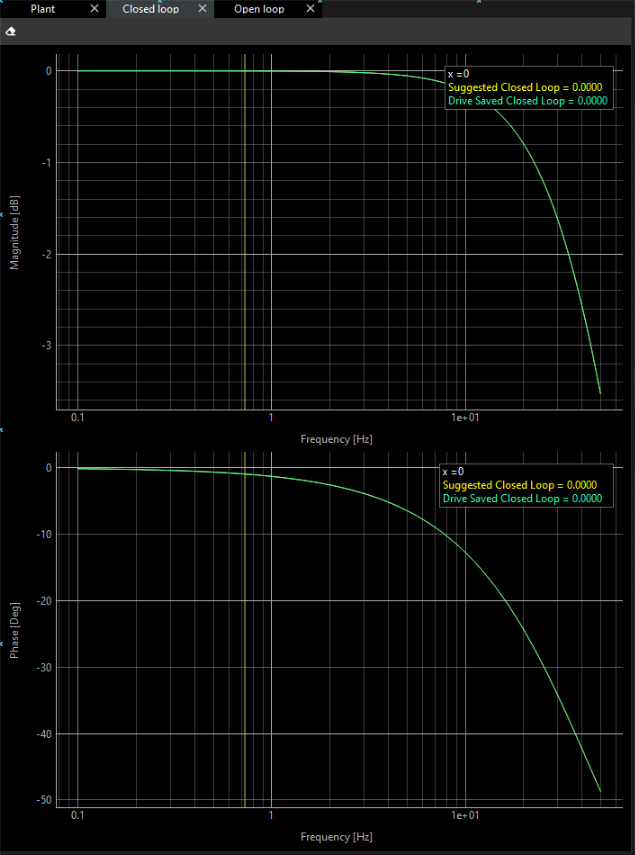
Verification

To compute a verification of your system, just click on the “Verification” button.

In this step, the main goal is checking how your actual system works with the current controller saved on the drive.

Let’s continue the example before.

Example

In order to make a verification, you can follow the steps below:

1. Modify the bandwidth value.

2. Click on the “Save to the Drive” button.

3. And click on the “Verification” button.

Finally we get a message below that tells us.

Charts are updated as well.

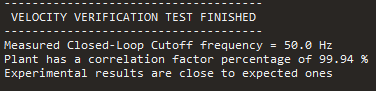
The terminal shows the quality (correlation factor) of the verification. This correlation factor compares the simulate results with the experimental ones.

Finally, some very specific applications, might require changing the excitation parameters. This can be done through the Advanced Options.

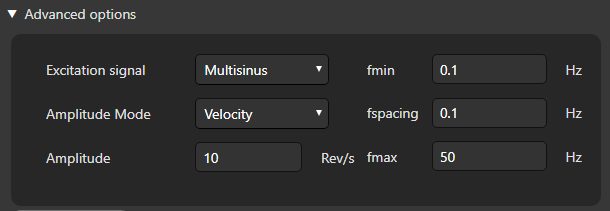
These parameters are:

• Excitation signal:

  • Multisinus

  • Sinesweep

  • Chirp

• Amplitude Mode: The only option is Velocity.

• Amplitude: The maximum speed of the motor.

• fmin: The minimum frequency that the plant is made.

• fspacing: The resolution of the frequency.

• fmax: The maximum frequency.

Finally, the simulation results are represented in closed-loop and open-loop.

In these charts there are no Experimental Closed Loop plots, just the estimated ones.

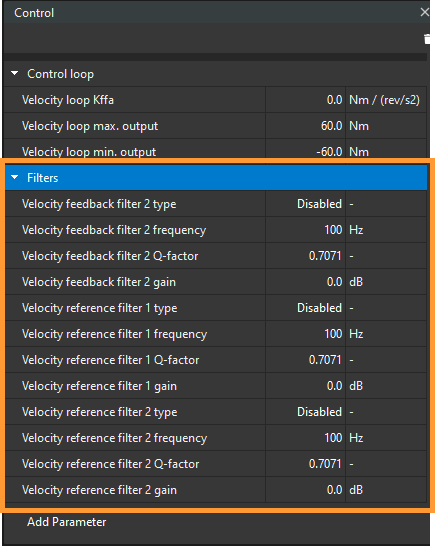
Finally, you can use two filters per signal for your system:

• Two for the velocity reference

• Two for the velocity feedback

You can available/disable at Control widget.

You can find further information at Filters and Offset section